Valôr assolût

Il valôr assolût o modul di un numar reâl al è il valôr no-negatîf dal numar, cence il segn. In pratiche, inte rete reâl, al rapresente la distance tra il numar e il zero.

Il valôr assolût come distance di un pont de rete reâl de origjine.

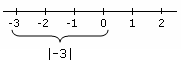
Definizion

Dât un numar reâl $x$, il so valôr assolût si indiche cun $|x|$ e si definìs come $$|x|={\begin{cases}x&{\text{se }}x\geq 0\\-x&{\text{se }}x<0.\end{cases}}$$ Si pues ancje scrivi $${\begin{aligned}|x|&=\max\{x;-x\}\\|x|&=x\cdot \mathbf {1} [x\geq 0]-x\cdot \mathbf {1} [x<0]\end{aligned}}$$ lì che si è usade la funzion indicadore $\mathbf {1} [\cdot ]$, che e vâl 1 se l'argoment al è vêr e 0 se al è fals. Ricuardant che la lidrîs cuadrade e je simpri positive o nule (par esempli, ${\sqrt {25}}=5$ ancje se $(-5)^{2}=25$), si à ancje $$|x|={\sqrt {x^{2}}}.$$

Proprietâts

Il valôr assolût al gjolt des proprietâts chi sot.

1. Il valôr assolût di un cualsisei numar reâl al è simpri plui grant o avuâl a zero,$$|a|=0\Leftrightarrow a=0.$$
2. Il modul dal prodot di doi numars al è simpri avuâl al prodot dai modui,$$|ab|=|a||b|\qquad \forall a,b\in \mathbb {R} .$$
3. Il valôr assolût di un numar reâl e dal so opuest a son avuâi,$$|-a|=|a|,\qquad \forall a\in \mathbb {R} .$$
4. Idempotence. Sint il modul un numar positîf, si à$${\bigl |}|a|{\bigr |}=|a|$$ven a stâi, il valôr assolût dal valôr assolût di un numar al è il stes valôr assolût.
5. Disavualitât triangolâr. Il valôr assolût de some di doi numars al è simpri minôr o avuâl ae some dai valôrs assolûts$$|a+b|\leq |a|+|b|\qquad \forall a,b\in \mathbb {R} .$$In particolâr, la avualitât e vâl se e dome se i doi numars a àn il stes segn (a concuardin). Al contrari, il segn di minôr al vâl in câs di discuardance.

Come conseguence de disavualitât triangolâr, si pues ancje scrivi$$|a-b|\geq {\bigl |}|a|-|b|{\bigr |}\qquad \forall a,b\in \mathbb {R} .$$

Dimostrazion: Dât che $a=(a-b)+b$, pe disavualitât triangolâr si pues scrivi$$|a|=|(a-b)+b|\leq |a-b|+|b|$$ven a stâi$$|a-b|\geq |a|-|b|.$$De stesse maniere, si pues provâ che$$|b-a|\geq |b|-|a|.$$Al baste cumò notâ che $|a-b|=|b-a|$ (pe proprietât 4) e che $|a|-|b|=-(|b|-|a|)$ e, duncje, ${\bigl |}|a|-|b|{\bigr |}$ al è avuâl o a $|a|-|b|$ o a $|b|-|a|$. Zontant ducj i risultâts si oten la disavualitât cirude.

La funzion valôr assolût

La funzion valôr assolût. La funzion valôr assolût $f(x):x\mapsto |x|$ e je une funzion reâl di variabil reâl. E je definide ecuivalentementri di une des formis viodudis prime o, doprant la funzion segn $\operatorname {sgn}(x)$, de forme $$|x|=x\operatorname {sgn}(x).$$ Come che si pues intuî de figure chi in bande, il valôr assolût al è une funzion continue su dut $\mathbb {R}$; liniâr a trats; diferenziabil par dut infûr dal pont $x=0$; monotoniche decressinte tal interval $(-\infty ,0]$ e monotoniche cressinte tal interval $[0,+\infty )$; convesse; pâr (i.e. $|x|=|-x|$) e duncje no invertibile. Esemplis di composizion dal valôr assolût.

Gjeneralizazion dal valôr assolût

La operazion valôr assolût di un numar reâl, e la sô interpretazion di misure di distance su la rete reâl, si puedin estindi a altris struturis matematichis. Par esempli, il modul di un numar complès $z=\Re \{z\}+\mathrm {j} \Im \{z\}$ al è dât di $$|z|={\sqrt {\Re ^{2}\{z\}+\Im ^{2}\{z\}}}$$ e al rapresente la distance dal pont $z$ de origjine dal plan complès. Un altri esempli al è la norme di un vetôr $n$-dimensionâl $\mathbf {v} =(v_{1},v_{2},\dots ,v_{n})$, ven a stâi $$\|\mathbf {v} \|={\sqrt {v_{1}^{2}+v_{2}^{2}+\dots +v_{n}^{2}}}.$$ Il numar reâl positîf $\|\mathbf {v} \|$ al è la misure de lungjece dal vetôr $\mathbf {v}$.

Bibliografie

• Wikipedia Contributors. Absolute value, in Wikipedia, The Free Encyclopedia, 20 avost 2015, <https://en.wikipedia.org/w/index.php?title=Absolute_value&oldid=673679090>.
• Contributori di Wikipedia, Valore assoluto, in Wikipedia, L'enciclopedia libera, 20 avost 2015, <https://it.wikipedia.org/w/index.php?title=Valore_assoluto&oldid=73289536>.